Polarisation/Magnetic Scattering

Models which define a scattering length density parameter can be evaluated as magnetic models. In general, the scattering length density (SLD = $\beta$) in each region where the SLD is uniform, is a combination of the nuclear and magnetic SLDs and, for polarised neutrons, also depends on the spin states of the neutrons.

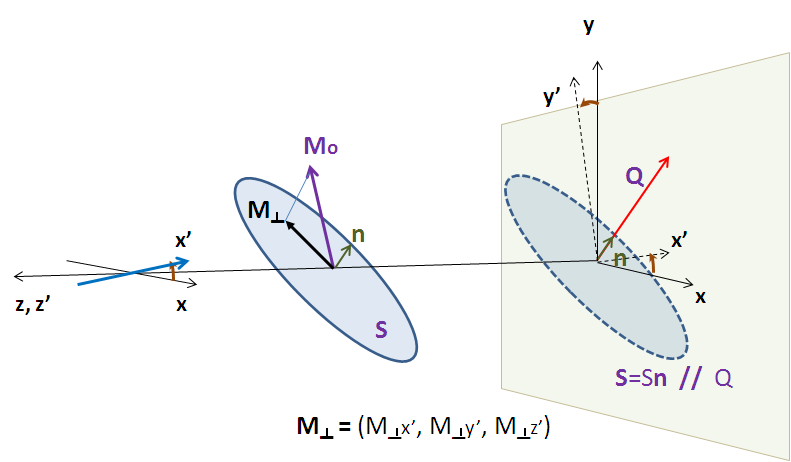
For magnetic scattering, only the magnetization component $\mathbf{M_\perp}$ perpendicular to the scattering vector $\mathbf{Q}$ contributes to the magnetic scattering length.

The magnetic scattering length density is then

$$\beta_M = \dfrac{\gamma r_0}{2\mu_B}\sigma \cdot \mathbf{M_\perp} = D_M\sigma \cdot \mathbf{M_\perp}$$

where $\gamma = -1.913$ is the gyromagnetic ratio, $\mu_B$ is the Bohr magneton, $r_0$ is the classical radius of electron, and $\sigma$ is the Pauli spin.

Assuming that incident neutrons are polarized parallel $(+)$ and anti-parallel $(-)$ to the $x'$ axis, the possible spin states after the sample are then:

• Non spin-flip $(+ +)$ and $(- -)$
• Spin-flip $(+ -)$ and $(- +)$

Each measurement is an incoherent mixture of these spin states based on the fraction of $+$ neutrons before ($u_i$) and after ($u_f$) the sample, with weighting:

$$\begin{split}-- &= (1-u_i)(1-u_f) \\ -+ &= (1-u_i)(u_f) \\ +- &= (u_i)(1-u_f) \\ ++ &= (u_i)(u_f)\end{split}$$

Ideally the experiment would measure the pure spin states independently and perform a simultaneous analysis of the four states, tying all the model parameters together except $u_i$ and $u_f$.

If the angles of the $Q$ vector and the spin-axis $x'$ to the $x$ - axis are $\phi$ and $\theta_{up}$, respectively, then, depending on the spin state of the neutrons, the scattering length densities, including the nuclear scattering length density $(\beta{_N})$ are

$$\beta_{\pm\pm} = \beta_N \mp D_M M_{\perp x'} \text{ for non spin-flip states}$$

and

$$\beta_{\pm\mp} = -D_M (M_{\perp y'} \pm iM_{\perp z'}) \text{ for spin-flip states}$$

where

$$\begin{split}M_{\perp x'} &= M_{0q_x}\cos(\theta_{up})+M_{0q_y}\sin(\theta_{up}) \\ M_{\perp y'} &= M_{0q_y}\cos(\theta_{up})-M_{0q_x}\sin(\theta_{up}) \\ M_{\perp z'} &= M_{0z} \\ M_{0q_x} &= (M_{0x}\cos\phi - M_{0y}\sin\phi)\cos\phi \\ M_{0q_y} &= (M_{0y}\sin\phi - M_{0x}\cos\phi)\sin\phi\end{split}$$

Here, $M_{0x}$, $M_{0x}$, $M_{0z}$ are the x, y and z components of the magnetization vector given in the laboratory xyz frame given by

$$\begin{split}M_{0x} &= M_0\cos\theta_M\cos\phi_M \\ M_{0y} &= M_0\sin\theta_M \\ M_{0z} &= -M_0\cos\theta_M\sin\phi_M\end{split}$$

and the magnetization angles $\theta_M$ and $\phi_M$ are defined in the figure above.

The user input parameters are:

sld_M0	$D_M M_0$
sld_mtheta	$\theta_M$
sld_mphi	$\phi_M$
up_frac_i	$u_i$ = (spin up)/(spin up + spin down) before the sample
up_frac_f	$u_f$ = (spin up)/(spin up + spin down) after the sample
up_angle	$\theta_\mathrm{up}$

Note

The values of the ‘up_frac_i’ and ‘up_frac_f’ must be in the range 0 to 1.

Document History

2015-05-02 Steve King

2017-11-15 Paul Kienzle

2018-06-02 Adam Washington