rectangular_prism

Rectangular parallelepiped with uniform scattering length density.

Parameter	Description	Units	Default value
scale	Scale factor or Volume fraction	None	1
background	Source background	cm-1	0.001
sld	Parallelepiped scattering length density	10-6Å-2	6.3
sld_solvent	Solvent scattering length density	10-6Å-2	1
length_a	Shorter side of the parallelepiped	Å	35
b2a_ratio	Ratio sides b/a	None	1
c2a_ratio	Ratio sides c/a	None	1
theta	c axis to beam angle	degree	0
phi	rotation about beam	degree	0
psi	rotation about c axis	degree	0

The returned value is scaled to units of cm^-1 sr^-1, absolute scale.

This model provides the form factor, \(P(q)\), for a rectangular prism.

Note that this model is almost totally equivalent to the existing parallelepiped model. The only difference is that the way the relevant parameters are defined here (\(a\), \(b/a\), \(c/a\) instead of \(a\), \(b\), \(c\)) which allows use of polydispersity with this model while keeping the shape of the prism (e.g. setting \(b/a = 1\) and \(c/a = 1\) and applying polydispersity to a will generate a distribution of cubes of different sizes).

Definition

The 1D scattering intensity for this model was calculated by Mittelbach and Porod (Mittelbach, 1961), but the implementation here is closer to the equations given by Nayuk and Huber (Nayuk, 2012). Note also that the angle definitions used in the code and the present documentation correspond to those used in (Nayuk, 2012) (see Fig. 1 of that reference), with \(\theta\) corresponding to \(\alpha\) in that paper, and not to the usual convention used for example in the parallelepiped model.

In this model the scattering from a massive parallelepiped with an orientation with respect to the scattering vector given by \(\theta\) and \(\phi\)

\[A_P\,(q) = \frac{\sin \left( \tfrac{1}{2}qC \cos\theta \right) }{\tfrac{1}{2} qC \cos\theta} \,\times\, \frac{\sin \left( \tfrac{1}{2}qA \cos\theta \right) }{\tfrac{1}{2} qA \cos\theta} \,\times\ , \frac{\sin \left( \tfrac{1}{2}qB \cos\theta \right) }{\tfrac{1}{2} qB \cos\theta}\]

where \(A\), \(B\) and \(C\) are the sides of the parallelepiped and must fulfill \(A \le B \le C\), \(\theta\) is the angle between the \(z\) axis and the longest axis of the parallelepiped \(C\), and \(\phi\) is the angle between the scattering vector (lying in the \(xy\) plane) and the \(y\) axis.

The normalized form factor in 1D is obtained averaging over all possible orientations

\[P(q) = \frac{2}{\pi} \int_0^{\frac{\pi}{2}} \, \int_0^{\frac{\pi}{2}} A_P^2(q) \, \sin\theta \, d\theta \, d\phi\]

And the 1D scattering intensity is calculated as

\[I(q) = \text{scale} \times V \times (\rho_\text{p} - \rho_\text{solvent})^2 \times P(q)\]

where \(V\) is the volume of the rectangular prism, \(\rho_\text{p}\) is the scattering length of the parallelepiped, \(\rho_\text{solvent}\) is the scattering length of the solvent, and (if the data are in absolute units) scale represents the volume fraction (which is unitless).

For 2d data the orientation of the particle is required, described using angles \(\theta\), \(\phi\) and \(\Psi\) as in the diagrams below, for further details of the calculation and angular dispersions see Oriented particles . The angle \(\Psi\) is the rotational angle around the long C axis. For example, \(\Psi = 0\) when the B axis is parallel to the x-axis of the detector.

For 2d, constraints must be applied during fitting to ensure that the inequality \(A < B < C\) is not violated, and hence the correct definition of angles is preserved. The calculation will not report an error, but the results may be not correct.

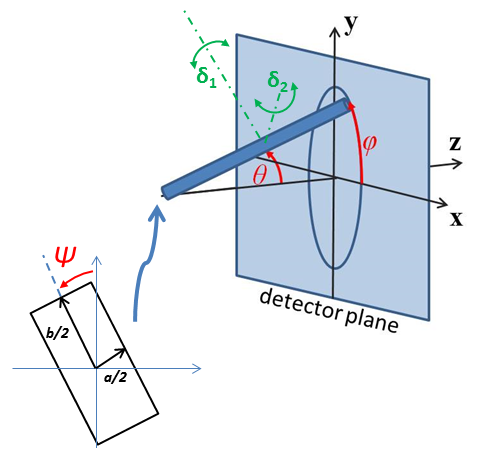
Fig. 72 Definition of the angles for oriented core-shell parallelepipeds. Note that rotation \(\theta\), initially in the \(xz\) plane, is carried out first, then rotation \(\phi\) about the \(z\) axis, finally rotation \(\Psi\) is now around the axis of the cylinder. The neutron or X-ray beam is along the \(z\) axis.

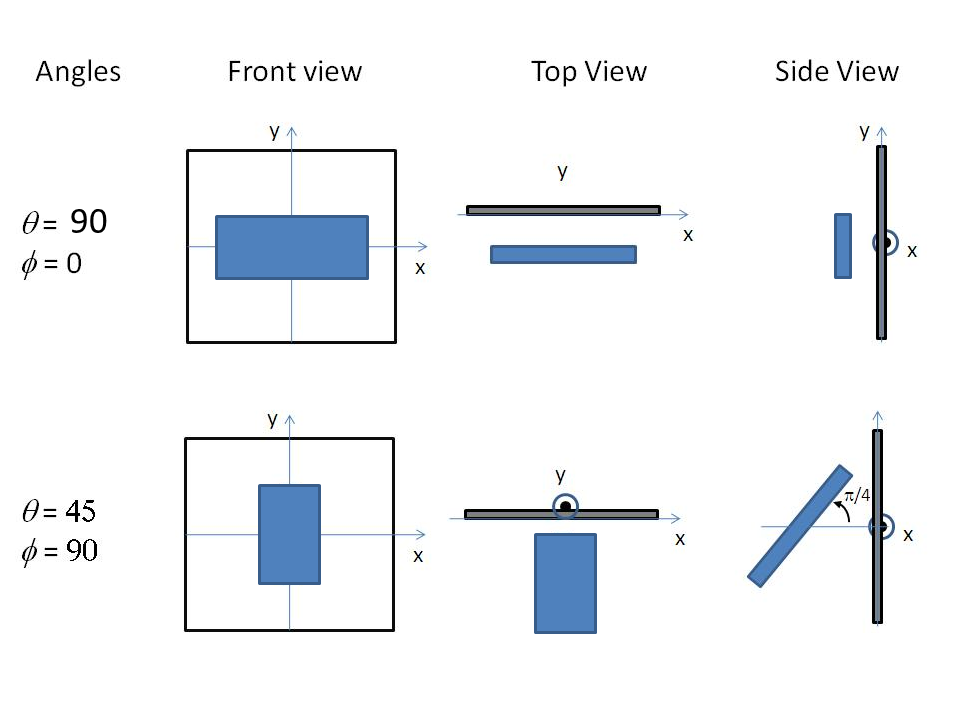
Fig. 73 Examples of the angles for oriented rectangular prisms against the detector plane.

Validation

Validation of the code was conducted by comparing the output of the 1D model to the output of the existing parallelepiped model.

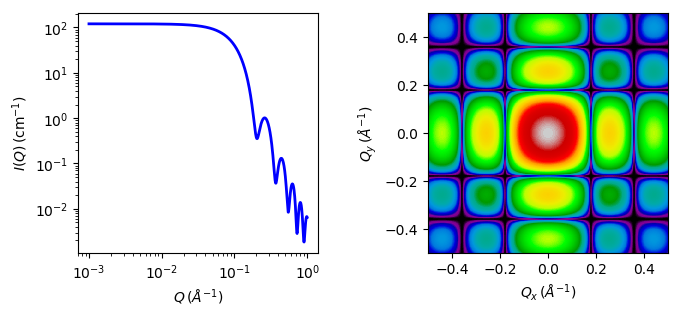
Fig. 74 1D and 2D plots corresponding to the default parameters of the model.

Source

rectangular_prism.py \(\ \star\ \) rectangular_prism.c \(\ \star\ \) gauss76.c

References

1. P Mittelbach and G Porod, Acta Physica Austriaca, 14 (1961) 185-211
2. R Nayuk and K Huber, Z. Phys. Chem., 226 (2012) 837-854
3. 12. Onsager, Ann. New York Acad. Sci., 51 (1949) 627-659

Authorship and Verification

• Author:
• Last Modified by:
• Last Reviewed by: