spherical_sld
Spherical SLD intensity calculation
| Parameter | Description | Units | Default value |
|---|---|---|---|
| scale | Scale factor or Volume fraction | None | 1 |
| background | Source background | cm-1 | 0.001 |
| n_shells | number of shells (must be integer) | None | 1 |
| sld_solvent | solvent sld | 10-6Å-2 | 1 |
| sld[n_shells] | sld of the shell | 10-6Å-2 | 4.06 |
| thickness[n_shells] | thickness shell | Å | 100 |
| interface[n_shells] | thickness of the interface | Å | 50 |
| shape[n_shells] | interface shape | None | 0 |
| nu[n_shells] | interface shape exponent | None | 2.5 |
| n_steps | number of steps in each interface (must be an odd integer) | None | 35 |
The returned value is scaled to units of cm-1 sr-1, absolute scale.
Definition
Similarly to the onion, this model provides the form factor, P(q), for a multi-shell sphere, where the interface between the each neighboring shells can be described by the error function, power-law, or exponential functions. The scattering intensity is computed by building a continuous custom SLD profile along the radius of the particle. The SLD profile is composed of a number of uniform shells with interfacial shells between them.
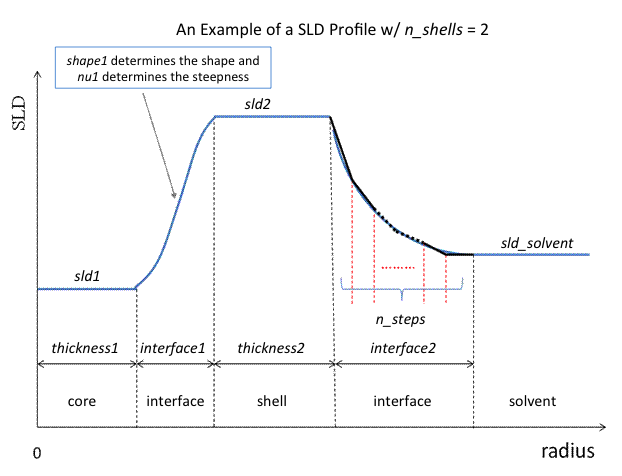
Fig. 90 Example SLD profile
Unlike the onion model (using an analytical integration), the interfacial shells here are sub-divided and numerically integrated assuming each sub-shell is described by a line function, with n_steps sub-shells per interface. The form factor is normalized by the total volume of the sphere.
Note
n_shells must be an integer. n_steps must be an ODD integer.
Interface shapes are as follows:
0: erf(νz)
1: Rpow(zν)
2: Lpow(zν)
3: Rexp(−νz)
4: Lexp(−νz)
The form factor P(q) in 1D is calculated by:
For a spherically symmetric particle with a particle density ρx(r) the sld function can be defined as:
so that individual terms can be calculated as follows:
Here we assumed that the SLDs of the core and solvent are constant in r. The SLD at the interface between shells, ρinteri is calculated with a function chosen by an user, where the functions are
Exp:
Power-Law:
Erf:
The functions are normalized so that they vary between 0 and 1, and they are constrained such that the SLD is continuous at the boundaries of the interface as well as each sub-shell. Thus B and C are determined.
Once ρinteri is found at the boundary of the sub-shell of the interface, we can find its contribution to the form factor P(q)
where
We assume ρinterj(r) is approximately linear within the sub-shell j.
Finally the form factor can be calculated by
For 2D data the scattering intensity is calculated in the same way as 1D, where the q vector is defined as
Note
The outer most radius is used as the effective radius for S(Q) when P(Q)∗S(Q) is applied.
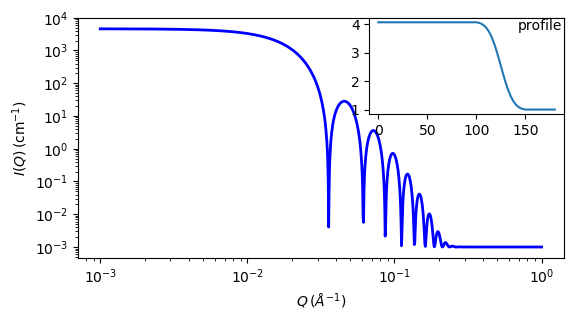
Fig. 91 1D plot corresponding to the default parameters of the model.
Source
spherical_sld.py
⋆ spherical_sld.c
⋆ sas_3j1x_x.c
⋆ sas_erf.c
⋆ polevl.c
References
- L A Feigin and D I Svergun, Structure Analysis by Small-Angle X-Ray and Neutron Scattering, Plenum Press, New York, (1987)
Authorship and Verification
- Author: Jae-Hie Cho Date: Nov 1, 2010
- Last Modified by: Paul Kienzle Date: Dec 20, 2016
- Last Reviewed by: Steve King Date: March 29, 2019