broad_peak

Broad Lorentzian type peak on top of a power law decay

Parameter Description Units Default value
scale Scale factor or Volume fraction None 1
background Source background cm-1 0.001
porod_scale Power law scale factor None 1e-05
porod_exp Exponent of power law None 3
lorentz_scale Scale factor for broad Lorentzian peak None 10
lorentz_length Lorentzian screening length Å 50
peak_pos Peak position in q Å-1 0.1
lorentz_exp Exponent of Lorentz function None 2

The returned value is scaled to units of cm-1 sr-1, absolute scale.

Definition

This model calculates an empirical functional form for SAS data characterized by a broad scattering peak. Many SAS spectra are characterized by a broad peak even though they are from amorphous soft materials. For example, soft systems that show a SAS peak include copolymers, polyelectrolytes, multiphase systems, layered structures, etc.

The d-spacing corresponding to the broad peak is a characteristic distance between the scattering inhomogeneities (such as in lamellar, cylindrical, or spherical morphologies, or for bicontinuous structures).

The scattering intensity \(I(q)\) is calculated as

\[I(q) = \frac{A}{q^n} + \frac{C}{1 + (|q - q_0|\xi)^m} + B\]

Here the peak position is related to the d-spacing as \(q_0 = 2\pi / d_0\).

\(A\) is the Porod law scale factor, \(n\) the Porod exponent, \(C\) is the Lorentzian scale factor, \(m\) the exponent of \(q\), \(\xi\) the screening length, and \(B\) the flat background.

For 2D data the scattering intensity is calculated in the same way as 1D, where the \(q\) vector is defined as

\[q = \sqrt{q_x^2 + q_y^2}\]
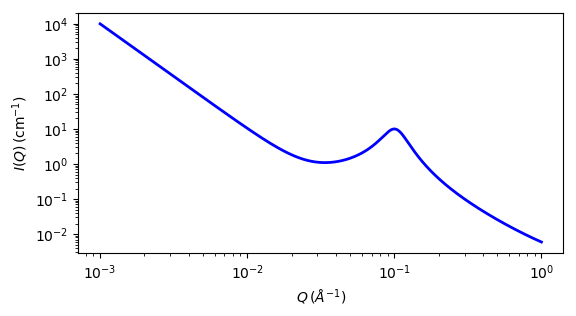
../../_images/broad_peak_autogenfig.png

Fig. 95 1D plot corresponding to the default parameters of the model.

Source

broad_peak.py

References

None.

Authorship and Verification

  • Author: NIST IGOR/DANSE Date: pre 2010
  • Last Modified by: Paul kienle Date: July 24, 2016
  • Last Reviewed by: Richard Heenan Date: March 21, 2016