core_multi_shell
This model provides the scattering from a spherical core with 1 to 10 concentric shell structures. The SLDs of the core and each shell are individually specified.
Parameter |
Description |
Units |
Default value |
|---|---|---|---|
scale |
Scale factor or Volume fraction |
None |
1 |
background |
Source background |
cm-1 |
0.001 |
sld_core |
Core scattering length density |
10-6Å-2 |
1 |
radius |
Radius of the core |
Å |
200 |
sld_solvent |
Solvent scattering length density |
10-6Å-2 |
6.4 |
n |
number of shells |
None |
1 |
sld[n] |
scattering length density of shell k |
10-6Å-2 |
1.7 |
thickness[n] |
Thickness of shell k |
Å |
40 |
The returned value is scaled to units of cm-1 sr-1, absolute scale.
Definition
This model is a trivial extension of the CoreShell function to a larger number of shells. The scattering length density profile for the default sld values (w/ 4 shells).
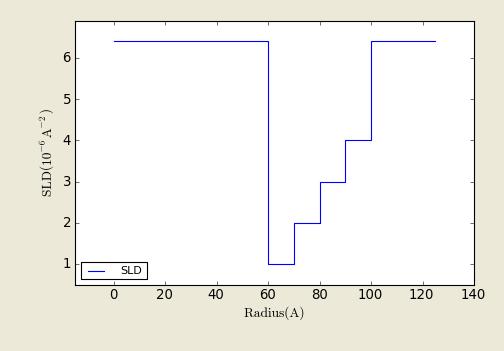
Fig. 77 SLD profile of the core_multi_shell object from the center of sphere out for the default SLDs.*
The 2D scattering intensity is the same as P(q) above, regardless of the orientation of the →q vector which is defined as
Note
Be careful! The SLDs and scale can be highly correlated. Hold as many of these parameters fixed as possible.
Note
The outer most radius (= radius + thickness) is used as the effective radius for S(Q) when P(Q)∗S(Q) is applied.
For information about polarised and magnetic scattering, see the Polarisation/Magnetic Scattering documentation.
Our model uses the form factor calculations implemented in a C-library provided by the NIST Center for Neutron Research [1].
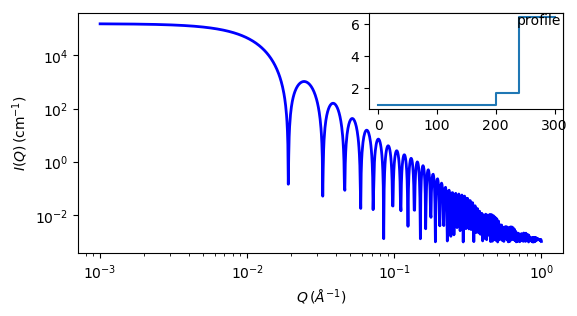
Fig. 78 1D plot corresponding to the default parameters of the model.
Source
core_multi_shell.py
⋆ core_multi_shell.c
⋆ sas_3j1x_x.c
References
Also see the core_shell_sphere model documentation and [2]
Authorship and Verification
Author: NIST IGOR/DANSE Date: pre 2010
Last Modified by: Paul Kienzle Date: September 12, 2016
Last Reviewed by: Paul Kienzle Date: September 12, 2016