correlation_length

Calculates an empirical functional form for SAS data characterized by a low-Q signal and a high-Q signal.

Parameter	Description	Units	Default value
scale	Scale factor or Volume fraction	None	1
background	Source background	cm-1	0.001
lorentz_scale	Lorentzian Scaling Factor	None	10
porod_scale	Porod Scaling Factor	None	1e-06
cor_length	Correlation length, xi, in Lorentzian	Å	50
porod_exp	Porod Exponent, n, in q^-n	None	3
lorentz_exp	Lorentzian Exponent, m, in 1/( 1 + (q.xi)^m)	None	2

The returned value is scaled to units of cm^-1 sr^-1, absolute scale.

Definition

The scattering intensity I(q) is calculated as

$$I(Q) = \frac{A}{Q^n} + \frac{C}{1 + (Q\xi)^m} + \text{background}$$

The first term describes Porod scattering from clusters (exponent = $n$) and the second term is a Lorentzian function describing scattering from polymer chains (exponent = $m$). This second term characterizes the polymer/solvent interactions and therefore the thermodynamics. The two multiplicative factors $A$ and $C$, and the two exponents $n$ and $m$ are used as fitting parameters. (Respectively porod_scale, lorentz_scale, porod_exp and lorentz_exp in the parameter list.) The remaining parameter $\xi$ (cor_length in the parameter list) is a correlation length for the polymer chains. Note that when $m=2$ this functional form becomes the familiar Lorentzian function. Some interpretation of the values of $A$ and $C$ may be possible depending on the values of $m$ and $n$.

For 2D data: The 2D scattering intensity is calculated in the same way as 1D, where the q vector is defined as

$$q = \sqrt{q_x^2 + q_y^2}$$

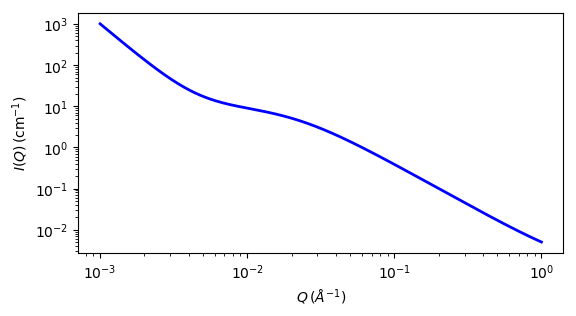
Fig. 99 1D plot corresponding to the default parameters of the model.

Source

correlation_length.py

References

1. B Hammouda, D L Ho and S R Kline, Insight into Clustering in Poly(ethylene oxide) Solutions, Macromolecules, 37 (2004) 6932-6937

Authorship and Verification

• Author: NIST IGOR/DANSE Date: pre 2010

• Last Modified by: Steve King Date: September 24, 2019

• Last Reviewed by: