flexible_cylinder
Flexible cylinder where the form factor is normalized by the volume of the cylinder.
Parameter |
Description |
Units |
Default value |
|---|---|---|---|
scale |
Scale factor or Volume fraction |
None |
1 |
background |
Source background |
cm-1 |
0.001 |
length |
Length of the flexible cylinder |
Å |
1000 |
kuhn_length |
Kuhn length of the flexible cylinder |
Å |
100 |
radius |
Radius of the flexible cylinder |
Å |
20 |
sld |
Cylinder scattering length density |
10-6Å-2 |
1 |
sld_solvent |
Solvent scattering length density |
10-6Å-2 |
6.3 |
The returned value is scaled to units of cm-1 sr-1, absolute scale.
This model provides the form factor, P(q), for a flexible cylinder where the form factor is normalized by the volume of the cylinder. Inter-cylinder interactions are NOT provided for.
where the averaging ⟨…⟩ is applied only for the 1D calculation
The 2D scattering intensity is the same as 1D, regardless of the orientation of the q vector which is defined as
Definitions
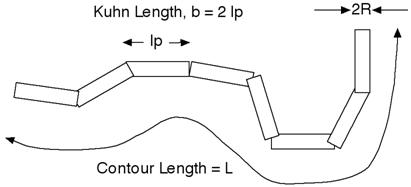
The chain of contour length, L, (the total length) can be described as a chain of some number of locally stiff segments of length lp, the persistence length (the length along the cylinder over which the flexible cylinder can be considered a rigid rod). The Kuhn length (b=2∗lp) is also used to describe the stiffness of a chain.
In the parameters, the sld and sld_solvent represent the SLD of the cylinder and solvent respectively.
Our model uses the form factor calculations in reference [1] as implemented in a c-library provided by the NIST Center for Neutron Research (Kline, 2006). This states:
‘Method 3 With Excluded Volume’ is used. The model is a parametrization of simulations of a discrete representation of the worm-like chain model of Kratky and Porod applied in the pseudocontinuous limit. See equations (13,26-27) in the original reference for the details.
Note
There are several typos in the original reference that have been corrected by Chen et al (WRC) [2]. Details of the corrections are in the reference below. Most notably
Equation (13): the term (1−w(QR)) should swap position with w(QR)
Equations (23) and (24) are incorrect; WRC has entered these into Mathematica and solved analytically. The results were then converted to code.
Equation (27) should be q0=max(a3/(Rg2)1/2,3) instead of max(a3∗b(Rg2)1/2,3)
The scattering function is negative for a range of parameter values and q-values that are experimentally accessible. A correction function has been added to give the proper behavior.
This is a model with complex behaviour depending on the ratio of L/b and the reader is strongly encouraged to read reference [1] before use. In particular, the cylinder form factor used as the limiting case for long narrow rods will not be exactly correct for short and/or wide rods.
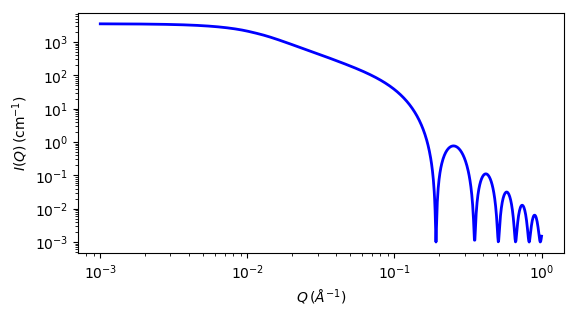
Fig. 29 1D plot corresponding to the default parameters of the model.
Source
flexible_cylinder.py
⋆ flexible_cylinder.c
⋆ wrc_cyl.c
⋆ sas_J1.c
⋆ polevl.c
References
J S Pedersen and P Schurtenberger. Scattering functions of semiflexible polymers with and without excluded volume effects. Macromolecules, 29 (1996) 7602-7612
W R Chen, P D Butler and L J Magid, Incorporating Intermicellar Interactions in the Fitting of SANS Data from Cationic Wormlike Micelles. Langmuir, 22(15) 2006 6539-6548
Authorship and Verification
Author:
Last Modified by:
Last Reviewed by: Steve King Date: March 6, 2020