pringle
The Pringle model provides the form factor, P(q), for a ‘pringle’ or ‘saddle-shaped’ disc that is bent in two directions.
Parameter |
Description |
Units |
Default value |
|---|---|---|---|
scale |
Scale factor or Volume fraction |
None |
1 |
background |
Source background |
cm-1 |
0.001 |
radius |
Pringle radius |
Å |
60 |
thickness |
Thickness of pringle |
Å |
10 |
alpha |
Curvature parameter alpha |
None |
0.001 |
beta |
Curvature paramter beta |
None |
0.02 |
sld |
Pringle sld |
10-6Å-2 |
1 |
sld_solvent |
Solvent sld |
10-6Å-2 |
6.3 |
The returned value is scaled to units of cm-1 sr-1, absolute scale.
Definition
The form factor for this bent disc is essentially that of a hyperbolic paraboloid and calculated as
where
and Δρ is ρpringle−ρsolvent, V is the volume of the disc, ψ is the angle between the normal to the disc and the q vector, d and R are the “pringle” thickness and radius respectively, α and β are the two curvature parameters, and Jn is the nth order Bessel function of the first kind.
Fig. 34 Schematic of model shape (Graphic from Matt Henderson, matt@matthen.com)
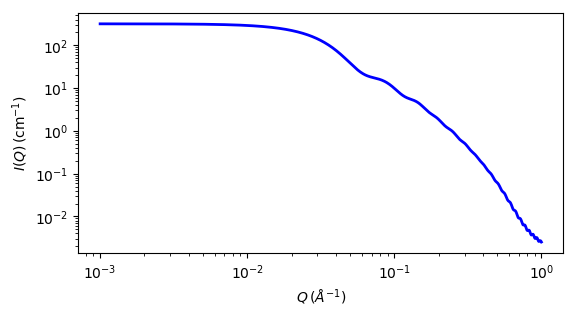
Fig. 35 1D plot corresponding to the default parameters of the model.
Source
pringle.py
⋆ pringle.c
⋆ gauss76.c
⋆ sas_JN.c
⋆ sas_J1.c
⋆ sas_J0.c
⋆ polevl.c
Reference
Karen Edler, Universtiy of Bath, Private Communication. 2012. Derivation by Stefan Alexandru Rautu.
Onsager, Ann. New York Acad. Sci., 51 (1949) 627-659
Authorship and Verification
Author: Andrew Jackson Date: 2008
Last Modified by: Wojciech Wpotrzebowski Date: March 20, 2016
Last Reviewed by: Andrew Jackson Date: September 26, 2016