sphere
Spheres with uniform scattering length density
Parameter |
Description |
Units |
Default value |
|---|---|---|---|
scale |
Scale factor or Volume fraction |
None |
1 |
background |
Source background |
cm-1 |
0.001 |
sld |
Layer scattering length density |
10-6Å-2 |
1 |
sld_solvent |
Solvent scattering length density |
10-6Å-2 |
6 |
radius |
Sphere radius |
Å |
50 |
The returned value is scaled to units of cm-1 sr-1, absolute scale.
For information about polarised and magnetic scattering, see the Polarisation/Magnetic Scattering documentation.
Definition
The 1D scattering intensity is calculated in the following way (Guinier, 1955)
where scale is a volume fraction, V is the volume of the scatterer, r is the radius of the sphere and background is the background level. sld and sld_solvent are the scattering length densities (SLDs) of the scatterer and the solvent respectively, whose difference is Δρ.
Note that if your data is in absolute scale, the scale should represent the volume fraction (which is unitless) if you have a good fit. If not, it should represent the volume fraction times a factor (by which your data might need to be rescaled).
The 2D scattering intensity is the same as above, regardless of the orientation of →q.
Validation
Validation of our code was done by comparing the output of the 1D model to the output of the software provided by the NIST (Kline, 2006).
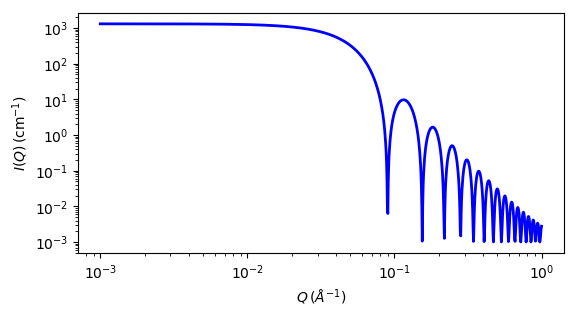
Fig. 89 1D plot corresponding to the default parameters of the model.
Source
sphere.py
⋆ sphere.c
⋆ sas_3j1x_x.c
References
A Guinier and G. Fournet, Small-Angle Scattering of X-Rays, John Wiley and Sons, New York, (1955)
Authorship and Verification
Author:
Last Modified by:
Last Reviewed by: S King and P Parker Date: 2013/09/09 and 2014/01/06