micromagnetic_FF_3D

Field-dependent magnetic microstructure around imperfections in bulk ferromagnets

Parameter	Description	Units	Default value
scale	Scale factor or Volume fraction	None	1
background	Source background	cm-1	0.001
radius	Structural radius of the core	Å	50
thickness	Structural thickness of shell	Å	40
nuc_sld_core	Core scattering length density	10-6Å-2	1
nuc_sld_shell	Scattering length density of shell	10-6Å-2	1.7
nuc_sld_solvent	Solvent scattering length density	10-6Å-2	6.4
mag_sld_core	Magnetic scattering length density of core	10-6Å-2	1
mag_sld_shell	Magnetic scattering length density of shell	10-6Å-2	1.7
mag_sld_solvent	Magnetic scattering length density of solvent	10-6Å-2	3
hk_sld_core	Anisotropy field of defect	10-6Å-2	1
Hi	Effective field inside the material	T	2
Ms	Volume averaged saturation magnetisation	T	1
A	Average exchange stiffness constant	pJ/m	10
D	Average DMI constant	mJ/m^2	0
up_i	Polarisation incoming beam	None	0.5
up_f	Polarisation outgoing beam	None	0.5
alpha	Inclination of field to neutron beam	None	90
beta	Rotation of field around neutron beam	None	0

The returned value is scaled to units of cm^-1 sr^-1, absolute scale.

Definition This model is a micromagnetic approach to analyse the SANS that arises from nanoscale variations in the magnitude and orientation of the magnetization in bulk ferromagnets in the approach to magnetic saturation (single domain state). Typical materials are cold-worked elemental magnets, hard and soft magnetic nanocomposites, amorphous alloys and precipitates in magnetic steel [5]. The magnetic SANS depends on the magnetic interactions, the magnetic microstructure (defect/particle size, magnetocrystalline anisotropy, saturation magnetisation) and on the applied magnetic field. As shown in [6] near magnetic saturation the scattering cross-section can be evaluated by means of micromagnetic theory

\[I(\mathbf{Q}) = I_{nuc} + I_{mag}(\mathbf{Q},H),\]

with the field-independent nuclear and magnetic SANS cross section (due to nanoscale spatial variations of the magnetisation).

\[I_{mag}(\mathbf{Q},H)= S_K(Q) R_K(\mathbf{Q}, H_i) + S_M(Q) R_M(\mathbf{Q}, H_i),\]

with \(H_i\) the internal field, i.e. the external magnetic field corrected for demagnetizing effects and the influence of the magnetodipolar field and of the magnetic anisotropy [3]. This magnetic field dependence of the scattering reflects the increasing magnetisation misalignment with decreasing externally applied magnetic field with a contribution \(S_K \times R_K\) due to perturbations around magnetic anisotropy fields and a term \(S_M \times R_M\) related to magnetostatic fields. The magnetic moments decorate perturbations in the microstructure (precipitates, grain boundaries etc). The anisotropy-field function \(S_K\) depends on the Fourier transform of the magnetic anisotropy distribution (strength and orientation) in the material, and the scattering function of the longitudinal magnetisation \(S_M\) reflects the variations of the saturation magnetisation, e.g. jumps at the particle-matrix interface. \(R_K\) and \(R_M\) denote the micromagnetic response functions that describe the magnetisation distribution around a perturbation in magnetic anisotropy and flucutations in the saturation magnetisation value.

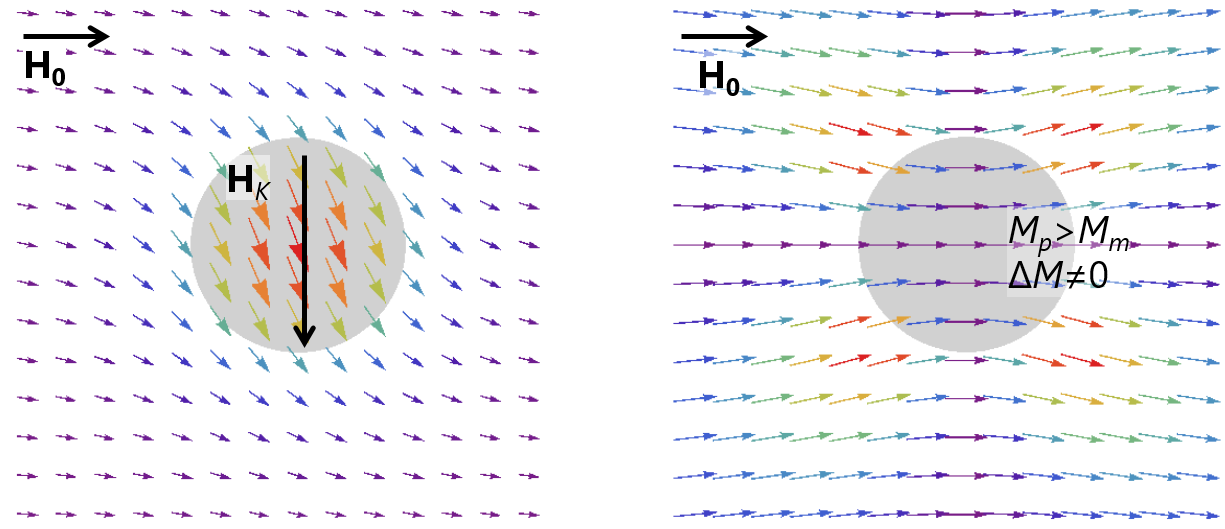
Fig. 83 Magnetisation distribution around (left) a particle with magnetic easy axis in the vertical direction and (right) a precipitation with a magnetisation that is higher than the matrix phase.

The micromagnetic response functions depend on magnetic material parameters \(M_S\): average saturation magnetisation of the material, \(H_i\): the internal magnetic field, \(A\) the average exchange-stiffness constant. In the vicinity of lattice imperfection in ferromagnetic materials, antisymmetric Dzyaloshinskii–Moriya interaction (DMI) can occur due to the local structural inversion symmetry breaking [1]. DMI with strength \(D\) can give rise to nonuniform spin textures resulting in a polarization-dependent asymmetric scattering term for polycrystalline ferromagnetic with a centrosymmetric crystal structure [6]. We assume (for simplicity) an isotropic microstructure (for \(S_M\)) and random orientation of magnetic easy axes (additionally for \(S_K\)) such that the contributions of the magnetic microstructure only depend on the magnitude of \(q\). Considerations for a microstructure with a prefered orientation (texture) can be found in [2]. In the code the averaging procedure over the random anisotropy is explicitely performed. A specific orientation distribution can be implemented by rewriting the model.

The magnetic field is oriented with an inclination of \(\alpha\) to the neutron beam and rotated by \(\beta\). The model for the nuclear scattering amplitude, saturation magnetisation is based on spherical particles with a core shell structure. For simplicity, only the core has an effective anisotropy, that is varying randomly in direction from particle to particle. The effect of different, more complex spatial profiles of the anisotropy can be seen in [4]. The magnetic scattering length density (SLD) is defined as \(\rho_{\mathrm{mag}}=b_H M_S\), where \(b_H= 2.91*10^{8}A^{-1}m^{-1}\) and \(M_S\) is the saturation magnetisation (in \(A/m\)).

The fraction of “upward” neutrons before (‘up_frac_i’) and after the sample (‘up_frac_f’) must range between 0 to 1, with 0.5 denoting an unpolarised beam. Note that a fit may result in a negative magnetic SLD, and hence magnetisation, when the polarisation state is inverted, i.e. if you have analysed for a \(I_{00}\) state wheras your data are \(I_{11}\). The model allows to construct the 4 spin-resolved cross sections (non-spin-flip \(I_{00}\), \(I_{11}\) and spin-flip, here \(I_{01}=I_{10}\)), half-polarised SANS (SANSpol, incoming polarised beam \(I_0\) and \(I_1\), no analysis after sample ‘up_frac_f’$=0.5$), and unpolarised beam (‘up_frac_i’$=$’up_frac_f’$=0.5$). Differences and other combinations between polarised scattering cross section, e.g. to obtain the nuclear-magnetic interference scattering, or subtraction of the residual scattering of the high field reference state can be constructed with a custom model (Fitting> Add/Multiply Model) and using approbriate scales. For dense systems, special care has to be taken as the nculear structure factor (arrangement of particles) does not need to be identical with the magnetic microstructure e.g. local textures and correlations between easy axes (see [7] for further details). The use of structure model is therefore strongly discouraged. Better \(I_{nuc}\), \(S_K\) and \(S_M\) are fit independent from each other in a model-free way.

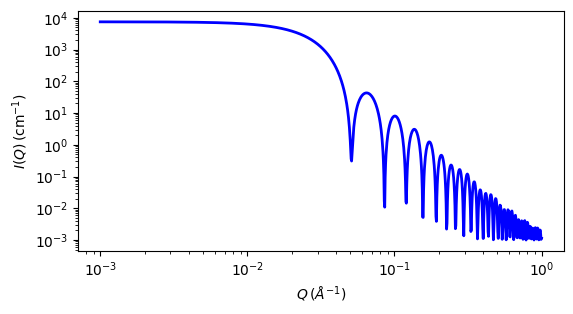
Fig. 84 1D plot corresponding to the default parameters of the model.

Source

micromagnetic_FF_3D.py \(\ \star\ \) micromagnetic_FF_3D.c \(\ \star\ \) magnetic_functions.c \(\ \star\ \) gauss76.c \(\ \star\ \) core_shell.c \(\ \star\ \) sas_3j1x_x.c

References

[1]

1. Arrott, J. Appl. Phys. 34, 1108 (1963).

[2]

10. Weissmueller et al., Phys. Rev. B 63, 214414 (2001).

[3]

J.-P. Bick et al., Appl. Phys. Lett. 102, 022415 (2013).

[4]

1. Michels et al., Phys. Rev. B 82, 024433 (2010).

[5]

1. Michels, J. Phys.: Condens. Matter 26, 383201 (2014).

[6] (1,2)

1. Michels et al., Phys. Rev. B 94, 054424 (2016).

[7]

4. Honecker, L. Fernandez Barguin, and P. Bender, Phys. Rev. B 101, 134401 (2020).

Authorship and Verification

• Author: Dirk Honecker Date: January 14, 2021

• Last Modified by: Dirk Honecker Date: September 23, 2024

• Last Reviewed by: